nicht auswendig lernen.

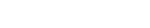
Ein Ingenieur, ein Physiker, ein Mathematiker und ein Philosoph machen eine Wanderung durch die schottischen Berge. Der Ingenieur ruft: "Seht, in Schottland sind die Kühe schwarz!" Der Physiker verbessert ihn: "Zumindest einige Kühe." Dazu der Mathematiker: "Zumindest eine Kuh." Und der Philosoph sagt: "Zumindest sehen wir, daß eine Kuh auf einer Seite das ist, was wir schwarz nennen."

Unter der Oberfläche
Ein Pfahl steht senkrecht im Boden eines Teichs und ragt aus dem Wasser. Im Boden steckt 1/4 des Pfahls, 1/3 wird vom Wasser bedeckt und 2,5 Meter sind oberhalb der Wasseroberfläche.Welche Länge hat der gesamte Pfahl?
Lösung: 6 Meter

Heimwerker
Ein Mann verlegt die Panelen für einen Parkettboden. Am 1. Tag verbraucht er 1/4 der Gesamtmenge, am 2. Tag 1/3 der Restmenge und am 3. Tag die Hälfte der neuen Restmenge. Es bleiben ihm 90 Panelen übrig.Wieviele Panelen hatte der Heimwerker anfangs?
Lösung: 360 Panelen

Gegen den Strom
Ein Motorboot fährt mit der Strömung in 24 Sekunden 120 Meter. Fährt es entgegen der Strömung, so braucht es für die gleiche Strecke 40 Sekunden. Wie schnell sind jeweils das Boot und die Strömung?Lösung: Das Motorboot fährt 14,4 km/h und die Strömung fliesst mit 3,6 km/h
Gleichseitiges Dreieck
Ein gleichseitiges Dreieck hat 3 gleich lange Seiten, die mit a benannt sind. Da die Seiten gleich lang sind, ergeben sich auch 3 gleich grosse Winkel, denn 360° : 3 = 60°Ziehen Sie dann ein Lot auf einer beliebigen Seite zum gegenüberliegenden Punkt, halbiert sich nicht nur die Seite, sondern auch der Winkel und es entsteht die Höhe des Dreiecks.

Es ging die Eins einmal auf Reisen,
die Freiheit von der Null zu preisen.
Und unterwegs trifft sie die Zehn,
kaum hatte sie die Zehn geseh'n:
"Bin nun befreit von dieser Nummer,
bereitet auch nur Gram und Kummer.
Wollt' ich mal multiplizieren,
sollte ich's Produkt verlieren,
auch den Summanden war's Verdruss,
dass man das Nichts addieren muss.
Doch fürchterlich die Division!
Als Teiler sorgt für Spott und Hohn,
die Null weil aus genannten Gründen
ist die Umkehrung nicht aufzufinden."
Entsetzt ob so viel Eitelkeit
ist die Zehn nun zum Disput bereit:
"Du glaubst, die Nummer Eins zu sein
und bildest dir etwas drauf ein?
Selbstgerecht und eigenmächtig,
schlank und etwas schmächtig
will die kleinste aller Ziffern
allein durch's Reich der Zahlen schiffern.
Ohne System wird nichts behagen
und alle Ziffern den Dienst versagen."
Die Eins gerät ins Grübeln:
"Wird's mir die Null etwa verübeln?"
Da kehrt sie um in ihr System
und sieht die Null auch schon dasteh'n.
"Komm mit mir auf unendlich' Reise!
Zusammen ist die beste Weise.
Auch ich hab's eingeseh'n.
Nur gemeinsam kann besteh'n,
was in Gegensätzlichkeit
ein kleines Intervall befreit."
Die Null, sie freut sich ehrlich:
"Wir sind doch beide unentbehrlich."
Es sagte mal das Polynom
zur linearen Funktion:
"Du bist doch nur ein armer Strich.
Viel mehr dagegen bin schon ich.
Bin elegant und schön geschwungen,
einfach als Konstrukt gelungen."
Die linear' Funktion, sie lacht:
"Weißt du, wie man Kurven macht?
Das, was man gern anguckt,
ist mein vielfaches Produkt.
Strich mal Strich mal Strich mal Strich...
Mehr, du Pfau, mehr bist du nich'.
Und der Fachmann kann, oh welch ein Segen,
dich mittels Division zerlegen."
Mathematik
Mathematik ist überall! Sie wird nicht auf dem Papier geboren, sondern in den Dingen der Welt. Mathe ist also keine Ausgeburt eines Vakuums sondern findet lediglich auf dem Papier ihre Niederschrift. Eine Übersetzung, wenn man so will. Oder eine Abschrift der Dinge, die uns umgeben. Verfasst in einer sehr knappen Sprache, die bestimmt nicht sehr klangvoll ist aber dafür umso effektiver.Das ist es, was manche Leute irritiert, wenn sie eine Tafel oder ein Papier voller Formeln sehen und sich sofort abwenden. Hinzu kommen manche Lehrer, die mechanisch und überaus geübt diese Übersetzung von links nach rechts und von oben nach unten quasi vorlesen und dann mit dem Satz schliessen: "Das ist doch alles ganz logisch!"
Und genau hier möchte ich ansetzen: Da Menschen unterschiedlich lernen - der eine schneller, der andere dafür gründlicher - gehe ich auf jeden einzeln ein. Im Einzelunterricht, mit Onlinenachhilfe, ganzheitlich oder etwas pointierter, wenn eine Prüfung ansteht. Rufen Sie mich einfach an!
ONLINE-TUTOR 0160 97319840
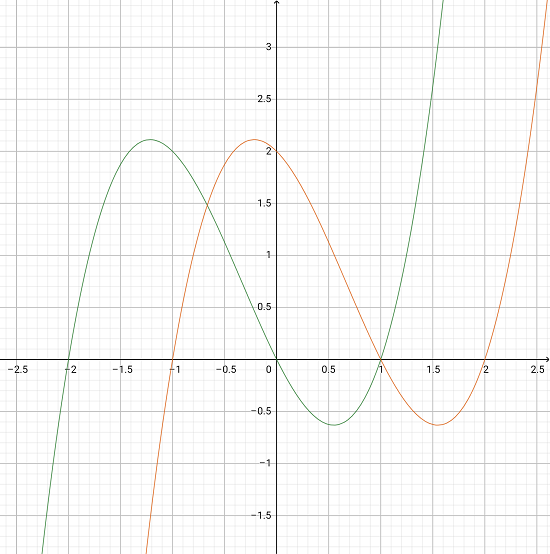
Brüche kürzen
Vergleicht man Brüche, verwendet man möglichst kleine Zahlen. Dazu müssen manche Brüche gekürzt werden. Man dividiert also den Zähler und den Nenner durch die gleiche Zahl und erhält einen Bruch, der zwar kleiner ist aber immer noch dasselbe Verhältnis aufweist wie der grosse Bruch. Dies geschieht so häufig wie möglich, um den neuen Bruch so klein wie möglich zu machen. So hat der Bruch 560 / 1120 das Verhältnis 1 zu 2 und stellt auch nichts anderes dar als 1 / 2 im gekürzten Bruch.
Geben Sie im Skript Zahlen mit maximal 5 Stellen ein. Sofern Sie versehentlich andere Zeichen - Buchstaben oder Sonderzeichen - eingeben, werden diese zwar gezählt, von der Funktion zur Division aber ignoriert. Beachten Sie auch, dass man durch 0 nicht dividieren kann!
Primzahlen
Eine Primzahl ist nur durch 1 und durch sich selber ganzzahlig teilbar. So kann man die 2 eben nur durch 1 oder durch 2 ganzzahlig teilen. Teilt man eine beliebige mehrstellige Zahl, dann hat diese mehrere Primzahlfaktoren. Zum Beispiel besteht die Zahl 2310 aus den Primzahlfaktoren 2, 3, 5, 7 und 11. Die Zahl 2600 hat lediglich die Primzahlfaktoren 2, 5 und 13. Die Grösse der Zahl entscheidet also nicht über die Anzahl der Primfaktoren.
Die Anzahl der Primzahlen ist unendlich. Man kann auch immer genau sagen, welche Zahl prim ist und welche nicht. Jedoch weiss man heute noch nicht so genau, welchem Prinzip die Verteilung folgt. Eine genaue Formel ist also noch nicht bekannt.
Teilbarkeit
Durch die Primzahlen stellt sich bald die Frage nach den Teilbarkeiten. Hat man zwei Zahlen, so sind diese natürlich beide durch 1 ganzzahlig teilbar. Sind beide Zahlen gerade Zahlen, dann ist der gemeinsame Teiler sowieso 2. Aber was ist mit 33 und 27? Beide Zahlen haben als grössten gemeinsamen Teiler die Zahl 3, da zwar 33 durch 11 aber eben 27 nicht durch 11 sondern durch 9 teilbar ist. Somit ist 11 und 9 beiden Zahlen nicht gemeinsam. Die 3 dagegen schon.
Im kleinsten gemeinsamen Vielfachen - also im kleinsten Produkt beider Zahlen - sind nun wieder beide Ausgangszahlen als Teiler enthalten. Es berechnet sich, indem man eine Zahl durch den ggT dividiert und dieses Ergebnis mit der anderen Zahl multipliziert.
Zufallszahlen
Ein Zufallsgenerator ist immer recht nützlich, um beliebige Werte zu erzeugen. Sucht man sich selber Werte aus, spielt das Unterbewusstsein manchmal Streiche und es entstehen Werte, die entweder besonders einfach zu dividieren sind oder auf andere Weise bequem sein könnten. Dieser Generator lässt 10 Ereignisse - sprich 10 Ziffern - zu, die bis zu 5 Positionen belegen können. Sie wählen also 7 Ereignisse auf 3 Positionen und erhalten z.B. 007, 000, 467 oder 777 als Ziffernfolgen.
Wenn Sie sich für die Anzahl der Ereignisse und der Positionen entschieden haben, ist es ratsam mehrmals auf "Berechnen" zu klicken, um sich vom Ablauf der Auswahl zu überzeugen. Beachten Sie auch, dass die erste Ziffer die 0 ist!
Modulo oder der ganzzahlige Rest
Es geht um die ganzzahlige Division bzw. den Rest, der eben nicht mehr ganzzahlig Teil des Dividenden ist. Die knappe Form y = a · x + b beschreibt, dass zum ganzzahligen Produkt a · x nun b addiert wird, um y komplett zu machen. Und dieser Teil b ist eben Modulo. Die Schreibweise - es gibt mehrere - könnte also10 mod 8 = 2 als Gleichung sein.
Zahlensysteme
Wir rechnen täglich mit dem Dezimalsystem. Und es ist auch völlig logisch: Die Ziffern - nicht die Zahlen - von 0 bis 9 werden zusammengenommen und sobald es mehr wird, rutschen wir eine Hierarchie weiter hoch. Aber es gibt noch mehr Zahlensysteme und diese werden häufig eingesetzt. So rechnet der Computer letztendlich immer im Binärsystem und ebenso im Rahmen der Informatik bietet sich das Hexadezimalsystem für die Darstellung großer Zahlen an.
Zeiten nehmen
Natürlich spielt die Zeit eine tragende Rolle. Jede Art des Ablaufs wird zeitlich gemessen und bedingt das Verhältnis, das aus Weg und Zeit besteht. In Koordinatensystemen verläuft die Zeit üblicherweise auf der x-Achse, während man den zurückgelegten Weg entlang der y-Achse abträgt und misst.
Im Skript können Sie maximal 5 Zeiten nehmen. Sobald die 5. Zeit überschritten ist, wird im oberen Output die 0 eingesetzt. Das Löschen der Zeiten ist jederzeit möglich.
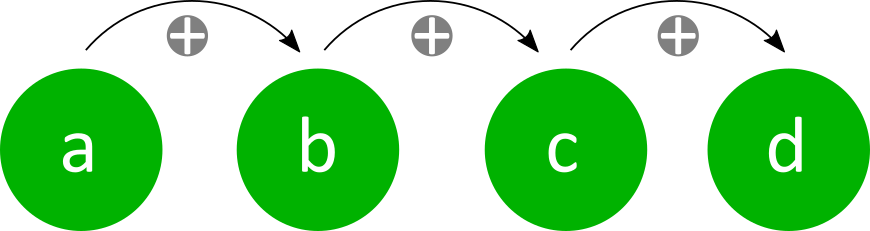
Die Quersumme
Addiert man die Ziffern einer Zahl - ganz gleich wie gross diese sein mag - ergibt sich die Quersumme. Nicht mit der Summation verwechseln, die eine Ziffern- und Zahlenfolge vorsieht. Also die Zahlen der Reihe nach. Bei der Quersumme ist keine Zahlenfolge vorgesehen. Übrigens eine nette Beschäftigung auf der Autobahn.
Im Skript können Sie maximal 10 Ziffern addieren. Eine Ziffernfolge, die einen Buchstaben oder ein Sonderzeichen enthält, gilt nicht als Zahl.
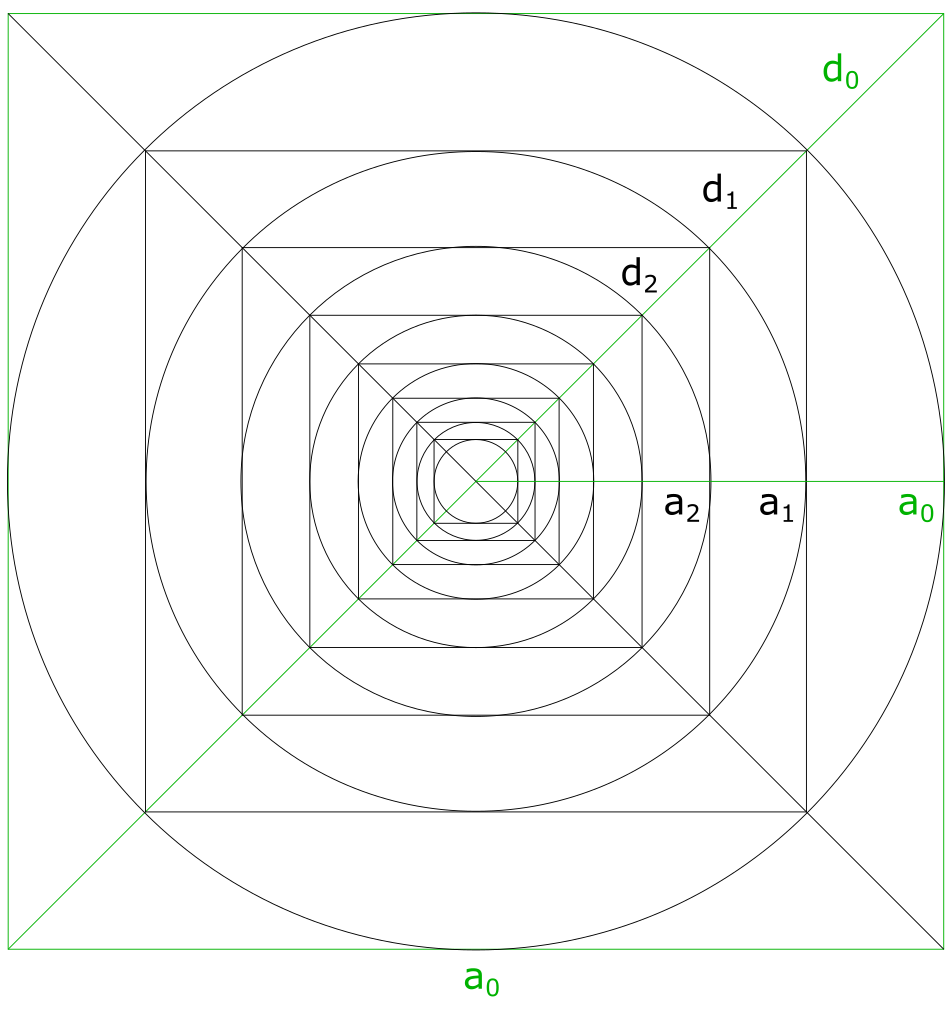
Zahlenfolgen
In einen Kreis wird immer wieder ein Quadrat einbeschrieben. Möchte man nun wissen, wie lang die Seite des n-ten Quadrats ist, so ist es bald nicht mehr möglich, dieses abzumessen. Hierbei handelt es sich um eine fortlaufende Berechnung. Geben Sie in das erste Feld die erste Seitenlänge als Ausgangswert ein und die Nummer des Index für das gesuchte Quadrat. Es werden die Länge der Seite und die Fläche berechnet.
Sobald die Eingaben irrelevante Ergebnisse liefern - etwa 0,0001 und kleiner - werden die Ausgaben auf 0 gesetzt. Ebenso bei falschen Eingaben, wie etwa Buchstaben oder Zeichen.
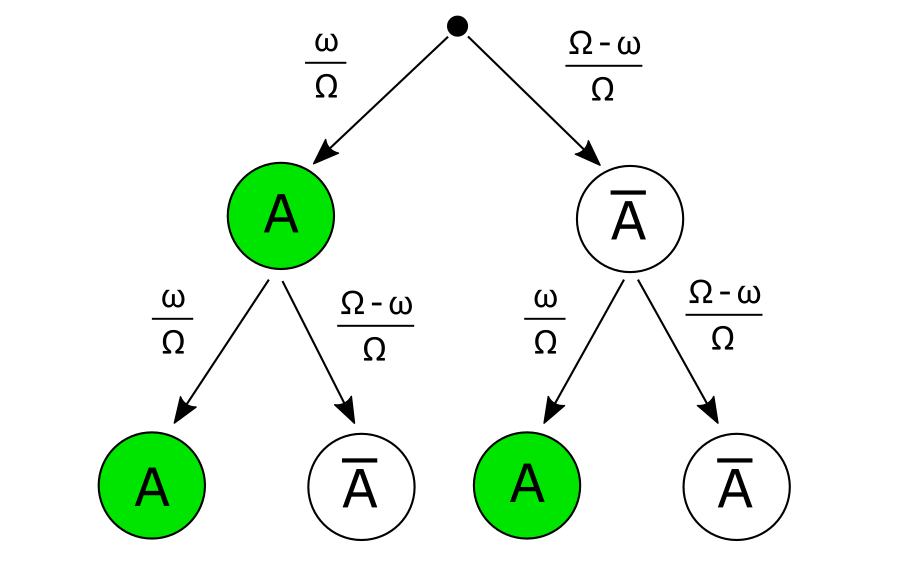
Das Gegenereignis
Wo es ein Ereignis gibt, da ist auch das Gegenereignis. Treffer oder nicht Treffer, Sein oder nicht sein, Plus oder Minus, 1 oder 0... Wir brauchen das Gegenereignis, um das Ganze zu erhalten. Wenn man so will, ist es im Sinne der Logik die Negation aller positiven - also aller gegebenen - Erscheinungen.ω + ( Ω - ω ) = Ω
Sobald also gefragt wird, wie gross die Wahrscheinlichkeit ist, bei 5 Versuchen 2 mal zu treffen, muss man 3 mal mit dem Gegenereignis rechnen. Und wir
freuen uns mächtig über...
2 + ( 5 - 2 ) = 5
Ein Körper
Ein Körper ist in der Algebra eine Menge. Diese Menge besitzt zwei innere Verknüpfungen, nämlich die Addition und die Multiplikation. Man nennt diese Verknüpfungen zweistellig, weil sie zwei Terme miteinander verbinden. Da die Terme auch negative Vorzeichen haben können, werden negative Zahlen addiert bzw. multipliziert. So handelt es sich bei der Subtraktion um eine Addition negativer Zahlen und bei der Division um die Multiplikation über den Dividenden hinaus mit Rest.
Take your time to solve the tasks! There is no timer, no function in the background which is counting.

Das Stadtticket
Eine Stadtverwaltung beklagt, dass nur 4% der Bürger das Stadtticket nutzen. Davon sind 98% Besserverdiener, denn 0,5% besitzen kein Stadtticket obwohl sie das Geld dazu hätten.
a) Mit welcher Wahrscheinlichkeit besitzt ein Bürger das Stadtticket, obwohl ihm das Geld dazu eigentlich fehlt?
b) Mit welcher Wahrscheinlichkeit hat ein Bürger kein Stadtticket, wenn man schon weiß, dass es ein Besserverdiener ist?
Derzeit kostet das Stadtticket 120 Euro und bei der jetzigen Menge an Abonnenten bräuchte die Verwaltung 3mal diese Einnahme. Jedoch haben 2000 Personen Interesse angemeldet.
a) Um wieviel Euro könnte das Ticket vergünstigt werden, wenn sich diese Interessenten tatsächlich für ein Abo entscheiden würden?
Lösungen: a) 0,08% b) ca. 11,3% a) 60 €

Prim oder nicht prim
Per Zufallsgenerator wird folgende Ziffernfolge definiert: 5; 3; 7; 2; 8; 5; 8; 3; 1; 1; 4; 7
a) Wie groß ist die Wahrscheinlichkeit, dass die gezogene Ziffer eine Primzahl sein wird?
b) Wie groß ist die Wahrscheinlichkeit, dass eine gezogene Ziffer eine Primzahl und zugleich die Ziffer drei sein wird?
c) Wie groß ist die Wahrscheinlichkeit, dass eine gezogene Ziffer die Drei sein wird, nachdem man schon weiß, dass die Ziehung eine Primzahl ergab?
Lösungen: a) 50% b) 16,67% c) 33,33%

Zug um Zug
Ein Zug hat eine Länge von 108 Metern und fährt mit 36 km/h. Ein anderer Zug ist 92 Meter lang und fährt 54 km/h. Sie fahren einander auf verschiedenen Gleisen einander entgegen.Wie lange wird es dauern, bis sie aneinander vorbei gefahren sind?
Lösung: 8 Sekunden
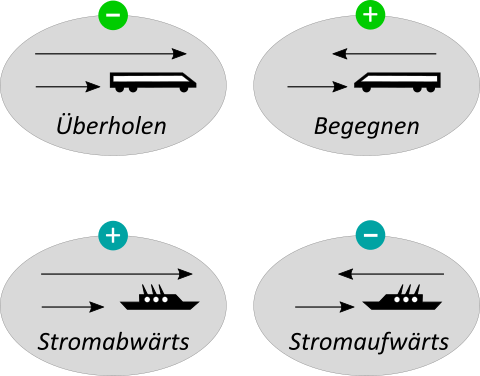
Faustformel
Eine Faustformel zum Verhalten zweier Geschwindigkeiten bietet sich fast an. Fällt etwas schwer - also Überholen oder gegen den Strom zu rudern - dann werden die Geschwindigkeiten voneinander abgezogen; Minus, negativ... Wird etwas erleichtert oder beschleunigt, dann addiert man die Geschwindigkeiten. Erleichterung verschafft z.B. der Rückenwind auf dem Fahrrad oder helfende Strömung. Begegnen sich zwei Züge, dann addiert man die Geschwindigkeiten wie etwa beim Aufprall. Natürlich auch dann, wenn sich zwei Autos auf der Hälfte zwischen A und B treffen sollten.

Vorzeichen
Eine negative Basis wird zur positiven Potenz, wenn der Exponent eine gerade ganze Zahl ist. Ist der Exponent jedoch eine ungerade Zahl, dann bleibt das Ergebnis negativ. (-2) · (-2) · (-2) = - 8 oder (-2) · (-2) = 4
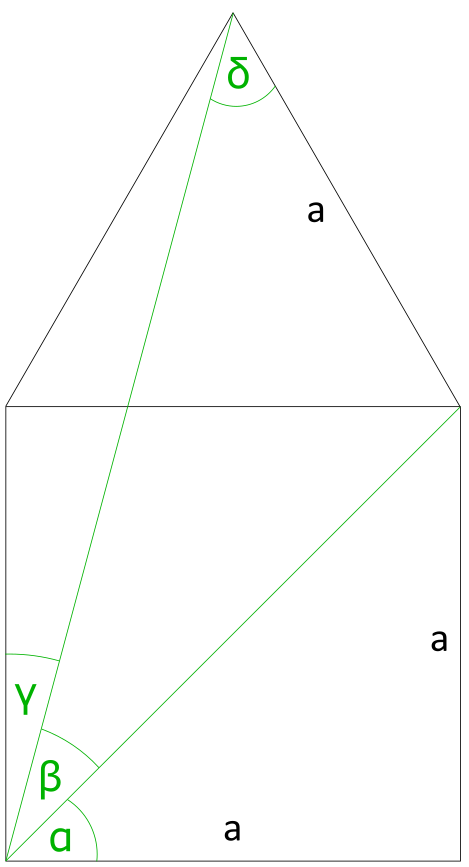
Winkel
Hierzu braucht nicht viel gesagt zu werden. Berechnen Sie einfach die angegebenen Winkel und alles ist gut.

Es ging die Drei einmal zur Hundert:
"Hundert, weißt' was mich schon lange wundert?
Du bist so groß und übermächtig
und ich so klein und niederträchtig.
Das Teilen will, vor allen Dingen,
uns nicht so Recht gelingen.
Ist meine Schuld, ich bin zu krumm."
"Kein Problem! Wir dreh'n es um."
sagt da die Hundert ganz entspannt.
Die Drei, sie hat den Trick auch gleich erkannt:
"Doch hoffentlich bemerkt jetzt keiner,
dadurch bin ich noch viel kleiner."
"Auch meine Gröss' ist jetzt dahin,
weil ich 'ne Kommastelle bin."

