Ein Geheimbund

Die Pythagoräer waren ein antiker, griechischer Geheimbund rund um ihren Anführer Pythagoras. Sie waren ganz versessen auf Mathematik und glaubten, Gott und das Universum mathematisch beschreiben zu können. Mit dem Universum hatten sie schon mal Recht, denn die Astrophysik kommt ohne Mathematik nicht aus. Die Pythagoräer waren aber keinesfalls entrückt oder gar eine Sekte. Sie beteiligten sich aktiv politisch und widersprachen der Doktrin ihrer Zeit nicht fundamental. Trotzdem gerieten sie scheinbar zwischen die Fronten, verließen Griechenland und siedelten sich in Süditalien an. Nicht allein deshalb hieß Süditalien zu dieser Zeit, also vor den Römern, wohl nicht untertrieben "Magna Graecia".

Oberstes Ordnungsprinzip war den Pythagoräern die Mathematik, genauer das Zahlenwerk. Mit Zahlen konnten sie die Welt und all ihre Dinglichkeiten hinreichend erklären. Quasi die Teile der Welt als Zahlen und das Ganze als das System derer.

So geheim, sonderbar und esoterisch sie auch gewesen sein mögen, legten sie doch einige Basics der Geometrie und Zahlentheorie, die heute noch Gültigkeit haben: Die Zahl 1 ist geometrisch der Punkt. Die Zahl 2 ist die Linie und die 3 die Fläche. Die Zahl 4 ist ein von vier Flächen (3), vier Linien (2) und vier Punkten (1) umschriebener Körper. Daher hatte die 10 für sie auch besondere Bedeutung, denn: 1 + 2 + 3 + 4 = 10.
Ferner unterteilten sie strikt gerade Zahlen und ungerade Zahlen. Das tun wir in der heutigen Zahlentheorie immer noch mit 2n oder 2n + 1. Gerade und ungerade Zahlen wurden damals allerdings mit Eigenschaften belegt, die heute gewiss nicht als wissenschaftlich durchgehen.

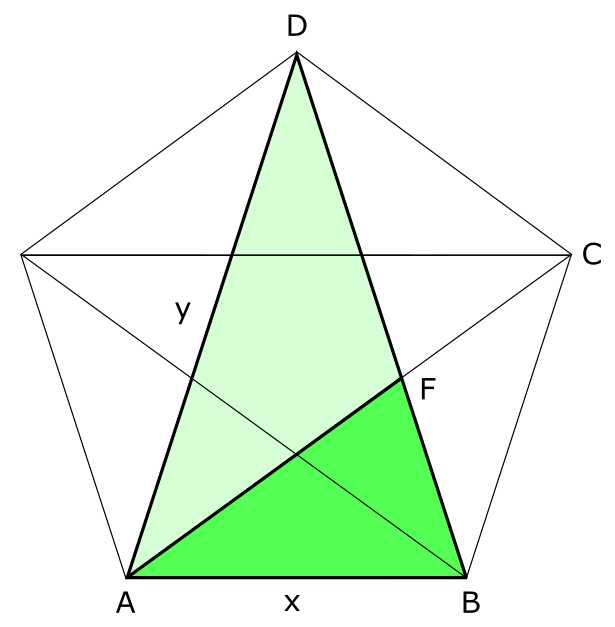
Ihr ebenfalls geheimes Zeichen war das Pentagramm, was auf griechisch etwa "Fünferlinie" heißt. Bei der Gelegenheit könnte man berechnen, wie groß der Winkel am Punkt A des Dreiecks BAF ist...

Es sagte mal das Polynom
zur linearen Funktion:
"Du bist doch nur ein armer Strich.
Viel mehr dagegen bin schon ich.
Bin elegant und schön geschwungen,
einfach als Konstrukt gelungen."
Die linear' Funktion, sie lacht:
"Weißt du, wie man Kurven macht?
Das, was man gern anguckt,
ist mein vielfaches Produkt.
Strich mal Strich mal Strich mal Strich...
Mehr, du Pfau, mehr bist du nich'.
Und der Fachmann kann, oh welch ein Segen,
dich mittels Division zerlegen."

Mathias Bleher 2024

Zwei Bäume...

...unterhalten sich: "Zu deiner Keimung war ich so alt wie du es jetzt bist. Seitdem ist dreimal so viel Zeit vergangen wie dein jetziges und somit mein damaliges Alter. Zusammen sind wir nun 100 Jahre alt." Wie alt sind die Bäume jetzt?

Ähnlichkeit und Proportion

Wieder nehme ich die Quintessenz der Lösung vorweg: Die Angaben beziehen sich auf die Basen der Dreiecke, die zusammen die Seitenlänge a ergeben.

Jetzt wird's genauer. Es verhalten sich 6 : z = 9 : x und somit kann man x mit 1,5z beschreiben. Ebenso 6 : z = 15 : y und auch y wird mit 2,5z dargestellt. Letztlich ist natürlich banal und reflexiv z = z, was dann zu 1,5z + 2,5z + z = a wird. Dann z = a : 5 die Beschreibung der ersten Basis anhand der gesamten Seitenlänge; ein Fünftel eben.

Wir wenden die Pythagoras für das Dreieck im Quadrat mit der Hypothenuse 15 an und statt y belegen wir 2,5z und auch die Variable z wird mit a : 5 belegt.

a² + y² = 15²

a² + ( 2,5z )² = 15²

a² + ( 2,5 ∙ ( a : 5 ))² = 15²

Der Gebrauch der Klammern ist hier wichtig! Nach Lösung der Gleichung ist 6√5 die Lösung und für die Fläche A(a) = ( 6√5 )² = 36 ∙ 5 = 180

Negative Zahlen

Negative Zahlen sind nicht deshalb entstanden, weil man irgendwann mal der Meinung war, die bittere Kälte hätte eine schlechte, negative Bezeichnung verdient.

Sie sind ein Spiegelbild an der Zahlengeraden. Der Spiegel ist die 0 und dieser projiziert die natürlichen Zahlen (1, 2, 3, usw.) auf die andere, negative Seite. Doch wozu das Ganze? Die sogenannte Gegenzahl ist in der Beweisführung der Mathematik besonders wichtig. Dabei geht es um das "additiv inverse Element", also...

a + (-a) = 0 und somit a = 0 + a

Zudem verlaufen Funktionen auch unterhalb der x-Achse des Koordinatensystems. Dieser Position wird man nur mit negativen Zahlen gerecht, etwa der Verlustzone einer Firma. Und generell ist es für den kaufmännischen Bereich wichtig, kurz und knapp "Soll" von "Haben" zu unterscheiden und es gibt noch andere Beispiele.

Wir möchten beweisen, dass "1" das kleinste Element der Menge der natürlichen Zahlen ohne 0 ist. M = { 1, 2, 3, ... }

Angenommen, es gäbe ein Element, das kleiner als 1 ist, dann läge es zwischen 0 und 1 also...

0 < x < 1

...dann wäre dieser Nachfolger von 0 mit...

0 + 1 = x

...definiert. Und der Vorgänger von 1 wäre dann...

1 - 1 = x

Wenn wir das gleichsetzen, dann erhalten wir...

0 + 1 = 1 - 1 also 1 = 0

...und das ist eine falsche Aussage! Somit gibt es in der Menge der natürlichen Zahlen ohne Null kein kleineres, und eben ganzzahliges, Element als 1.

In der Menge der "ganzen Zahlen" allerdings schon und diese ist auch in die andere Richtung unendlich. Übrigens ist -10 kleiner als -1, denn "je weiter links, umso kleiner". Unendlich kann also besonders groß oder besonders klein sein.

Up to top

Kopfrechnen

Kopfrechnen macht Spaß. Sobald eine zweistellige Zahl vorliegt, sollte distributiv vorgegangen werden. Allerdings bedeutet dies, dass man sich die Ergebnisse merken muss, um sie letztendlich zu addieren. Selbstverständlich können Sie Aufgaben überspringen oder sich das Ergebnis anzeigen lassen. Dann werden aber 10 % der Erfolgsquote abgezogen. Deshalb: In Ruhe rechnen! Es gibt kein Zeitlimit und keine Zeitfunktion im Hintergrund.

Im PopUp die Anzahl der Aufgaben. Und die Meldung gibt am Schluss an, wie oft gespickt wurde.

0

1 5 10 15 20 25 30 35 40

0

0

JavaScript und CSS in HTML: Mathias Bleher

Teilbarkeit

Durch die Primzahlen stellt sich bald die Frage nach den Teilbarkeiten. Hat man zwei Zahlen, so sind diese natürlich beide durch 1 ganzzahlig teilbar. Sind beide Zahlen gerade Zahlen, dann ist der gemeinsame Teiler sowieso 2. Aber was ist mit 33 und 27 usw.? Beide Zahlen haben als grössten gemeinsamen Teiler die Zahl 3, da zwar 33 durch 11 aber eben 27 nicht durch 11 sondern durch 9 teilbar ist. Somit ist 11 und 9 beiden Zahlen nicht gemeinsam. Die 3 dagegen schon.

1. Zahl

2. Zahl

Der ggT

Das kgV

JavaScript und CSS in HTML: Mathias Bleher

Im kleinsten gemeinsamen Vielfachen - also im kleinsten Produkt beider Zahlen - sind nun wieder beide Ausgangszahlen als Teiler enthalten. Es berechnet sich, indem man eine beliebige der beiden Zahlen durch den ggT dividiert und dieses Ergebnis mit der anderen Zahl multipliziert.

Brüche kürzen

Vergleicht man Brüche, verwendet man möglichst kleine Zahlen. Dazu müssen manche Brüche gekürzt werden. Man dividiert also den Zähler und den Nenner durch die gleiche Zahl und erhält einen Bruch, der zwar kleiner ist aber immer noch dasselbe Verhältnis aufweist wie der grosse Bruch. Dies geschieht so häufig wie möglich, um den neuen Bruch so klein wie möglich zu machen. So hat der Bruch 560 / 1120 das Verhältnis 1 zu 2 und stellt auch nichts anderes dar als 1 / 2 im gekürzten Bruch.

Geben Sie im Skript Zahlen mit maximal 5 Stellen ein. Sofern Sie versehentlich andere Zeichen - Buchstaben oder Sonderzeichen - eingeben, werden diese zwar gezählt, von der Funktion zur Division aber ignoriert. Beachten Sie auch, dass man durch 0 nicht dividieren kann! Dividiert man die 0 durch einen Wert, erhält man immer 0.

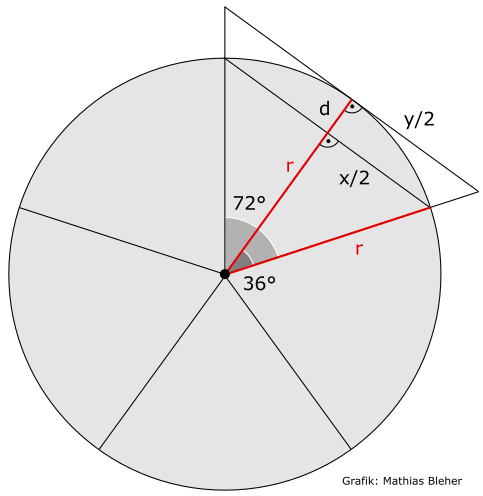
Wie π entsteht

Da wir von einem Fünfeck mit dem Sektorwinkel 72° ausgehen, ergeben sich 36° bei der Halbierung des Winkels. Diese ist nötig, um ein rechtwinkliges Dreieck zu erhalten. Damit kann man für die Seite x/2 den Sinus und für y/2 den Tangens anwenden. Das umbeschriebene n-Eck tangiert nämlich den Kreis. Beim Sinus ist der Radius des Kreises die Hypothenuse und beim Tangens ist der Radius des Kreises die Ankathete. Der Einfachheit halber kann man auch vom Einheitskreis mit dem Radius 1 ausgehen.

sin( 360° / 2n ) = ( x / 2 ) / r →
x = 2 ∙ sin( 360° / 2n ) ∙ r

Die Längen der Seiten x und y stehen also im Verhältnis zur Anzahl der Ecken eines beliebig großen n-Ecks. Man beachte auch, dass die gesamte Länge berechnet wurde und nicht mehr die Halbierung, wegen der Rechtwinkligkeit der Dreiecke.

tan( 360° / 2n ) = ( y / 2 ) / r →
y = 2 ∙ tan( 360° / 2n ) ∙ r

Möchte man nun die Umfänge berechnen, dann wird jeweils die berechnete Seitenlänge mit n für das n-Eck multipliziert.

U(x) = 5 ∙ x →
U(x) = 5 ∙ 2 ∙ sin( 360° / 2n ) ∙ r

U(y) = 5 ∙ y →
U(y) = 5 ∙ 2 ∙ tan( 360° / 2n ) ∙ r

Wie gesagt klemmt nun der Kreisumfang zwischen diesen beiden Umfängen des n-Ecks fest. Klar ist, dass der einbeschriebene Umfang kleiner als der Kreisumfang ist, aber der Kreisumfang kleiner als der umbeschriebene Umfang. Das kann man als Intervallschreibweise so notieren...

U(x) < 2πr < U(y)

Da wir uns für π isoliert interessieren und nicht für den gesamten Kreisumfang, dividieren wir die Ungleichung durch 2r und erhalten...

U(x)/2r < π < U(y)/2r

Und genau hier entsteht die Kreiszahl π auf unendlich viele Stellen nach bekanntem Anfang 3,14... Und der 14.03. ist der Tag der Zahl Pi, was uns rechnerisch nicht weitergeholfen hätte.

Zufallszahlen, Random

Sucht man sich selber Werte aus, spielt das Unterbewusstsein manchmal Streiche und es entstehen Werte, die entweder besonders einfach zu berechnen sind oder aus anderen Gründen im Hinterkopf herumgeistern. Etwa der Gerburtstag oder besonders wichtige Ereignisse Angehöriger. Daher ein unbestechlicher Zufallsgenerator.

Dieser Generator lässt 10 Ereignisse - sprich 10 Ziffern - zu, die bis zu 5 Positionen belegen können. Wählen Sie also z.B. 4 Ereignisse auf 3 Positionen, dann erhalten z.B. 004, 123, 414, 444 334 usw. als Ziffernfolgen.

Wenn Sie sich für die Anzahl der Ereignisse und der Positionen entschieden haben, ist es ratsam, mehrmals auf "Wählen!" zu klicken, um sich vom Ablauf der Auswahl zu überzeugen. Hier kann auch mehrmals die gleiche Abfolge entstehen und es sieht so aus, als täte sich nichts. Es versteht sich, dass sowohl die Ereignisse als auch die Positionen gewählt sein müssen.

Perpetua mobilia

Die Unmöglichkeit eines Perpetui mobilis steht wegen realer Bedingungen, wie Luftwiderstand oder Reibung des Materials, natürlich außer Frage. Daher gehen wir von einem "idealen, reibungsfreien System" aus, das ein Vakuum ist. Wir nehmen zwei unterschiedlich große Pendel. Diese sind unterschiedlich schwer und haben somit unterschiedliche Massen. Das größere Pendel mit mehr Masse hat auch mehr potenzielle Energie, die beim Schwingen in kinetische Energie (Bewegungsenergie) umgewandelt wird. Und umgekehrt, denn die Energie wird nicht verbraucht, sondern immer wieder umgewandelt. Beim kleineren Pendel ebenso, aber mit weniger Energie.

Die Pendel sind aber an unterschiedlich langen Aufhängungen angebracht. Theoretisch würden beide Pendel im idealen, reibungsfreien System unendlich lange schwingen. Jedoch sind die Geschwindigkeiten ihrer Schwingungen, also die Dauer ihrer einzelnen Schwingungen, unterschiedlich und hängen von der Länge der Aufhängung ab.

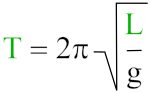
T die Schwingungsdauer ist die Zeit, die das Pendel benötigt, um eine vollständige Hin- und Herbewegung auszuführen,
L die Länge der Aufhängung wird gemessen vom Aufhängungspunkt bis zum Schwerpunkt des Pendelkörpers,
g die Erdbeschleunigung beträgt ungefähr 9,81 m/s² auf der Erdoberfläche.

Man erkennt, dass "L" für die Länge der Aufhängung die einzige Variable ist, während "2π" für die Kreisbewegung und "g" für die Gravitation konstant sind. Sie gelten somit für die unterschiedlichen Pendel gleichermaßen.

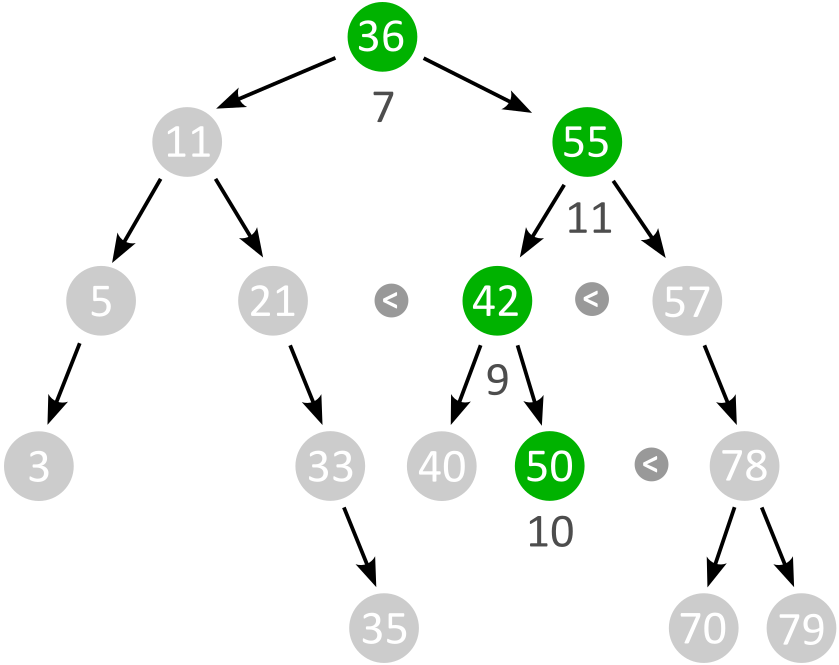
Die binäre Suche

Die binäre Suche ist eine besonders effiziente Art, durch Teilung bzw. Unterteilung in größer oder kleiner die Position eines gesuchten Elements zu erhalten.

Das Array muss aber in sortierter Form vorliegen. Entweder Zahlenwerte der Größe nach oder Buchstaben in alphabetischer Reihenfolge.

3	5	11	21	33	35	36	40	42	50	55	57	70	78	79
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

Hierbei wird das gesamte Array zunächst in der Mitte unterteilt. Die Anzahl der Positionen wird also einfach durch 2 dividiert. Da hier die Hälfte von 15 dezimal 7,5 ist, müssen wir abrunden, genauer wird der Rest ignoriert. Der Schrägstrich "/" steht nämlich für die ganzzahlige Division ohne Rest.

Wir haben also den Index 7 als Mitte mit 36. Sollte der gesuchte Wert jetzt auf dieser Mitte liegen, wäre die Suche beendet.

Falls nicht, wird entschieden, ob der gesuchte Wert kleiner - also links von der Mitte - oder größer - rechts von der Mitte - ist. Wir suchen die 50, die größer als 36 ist. Daher die Indices: ( 15 - 7 ) / 2 = 4 und dann 4 zum Anfang addiert ist 7 + 4 = 11 und da liegt die 55. Nun ist 50 kleiner als 55 und das Intervall wird wieder enger. ( 11 - 7 ) / 2 = 2, dann 7 + 2 = 9 mit dem Wert 42. Der gesuchte Wert 50 ist größer als 42 und ( 11 - 9 ) / 2 = 1, dann 9 + 1 = 10 mit dem Wert 50.

Exponentiell gewachsen

Tatsächlich eine Universalformel für alle Arten exponentiellen Wachstums, wie etwa Zinsen, Beschleunigungen, Pflanzen, Populationen etc., ist diese hier. Mit ihr lässt sich jeder Term, jede relevante Angabe eines Wachstumsprozesses berechnen. Kern des Themas ist der Grundwert, der sich ständig verändert. Durch die Potenzierung wird mit einer sich stets vergrößernden Basis gerechnet. Das unterscheidet den exponentiellen Wachstumsprozess vom linearen Verlauf, wo der Grundwert gleich bleibt.

Im Skript einfach den gesuchten Term auswählen, die restlichen Variablen belegen und auf "Berechnen" klicken. Beachten Sie, dass nur ganzzahlige Eingaben sinnvoll und gültig sind. Die Ausgabe habe ich auf zwei Dezimalstellen nach dem Komma begrenzt. Bei allzu großen Werten, die hier regelrecht den Rahmen sprengen, empfehle ich, mit kleineren Faktoren im gleichen Verhältnis zu rechnen. Diese kann man später wieder vervielfachen, liefern aber vorab das korrekte Ergebnis.

Princeps mathematicorum

Johann Carl Friedrich Gauß lebte von 1777 bis 1855 und wurde bereits zu Lebzeiten der "Fürst der Mathematiker" genannt. Bereits als Kind gelang ihm ein schnelles Verfahren, die Summe einer Zahlenreihe zu berechnen. Um die Summe einer arithmetischen Reihe, beispielsweise der natürlichen Zahlen von 1 bis 100, zu berechnen, hat er Paare gleicher Teilsumme gebildet, zum Beispiel 50 Paare mit der Summe 101, die aus 1 + 100, 2 + 99, …, 50 + 51 bestehen, wodurch sich 5050 als Ergebnis schneller als konventionell ergibt. Ob es sich dabei wirklich um die ihm aufgetragene Strafarbeit eines Lehrers handelte, kann ich nicht sagen. Jedenfalls sind solche Anekdoten gerne mal marginales Schmuckwerk.

Doch das ist nur ein kleines Fragment seiner Leistungen, die sich über die Mathematik hinaus auch auf die Vermessungstechnik, die Physik und die Astronomie erstreckten.

Im Skript können Sie - egal in welcher Reihenfolge - die Summe berechnen. Dabei muss natürlich nicht bei 1 angefangen werden. Viel interessanter sind die Intervalle dazwischen. Allerdings habe ich den Umfang auf dreistellige Zahlen begrenzt und glaube, es ist für den Hausgebrauch ausreichend.